Sampling

Drawing samples from a distribution $\pi$ is a problem that arises in many different fields. For example in generative AI, language models sample tokens from a learned probability distributions to generate new text. In computer graphics, many graphical engines randomly sample light paths bouncing around the scene to simulate realistic lighting. But what exactly does it mean for a computer or an algorithm to sample form a distribution? How can a deterministic machine like a modern computer sample "randomly" from a distribution?

Uniform Distribution

Let's start with the easiest distribution to sample from: the uniform distribution. In short, this distributions places equal probability on each $x$ in the state space. On most modern computers, one bit represents an atom of data or computation. So, if we want our computer to generate random samples, we would probably need it to be able to generate uniformly random bits. Let's assume we have a black box that does such a thing (this is not an unrealistic assumption since we have hardware random bit generators which generates random bits from physical process that produce entropy).

More formally, let $B \in \{0, 1\}$ be a random bit with $\mathbb{P}[B = 0] = \mathbb{P}[B = 1] = \frac{1}{2}$, and assume we can sample from $B$. Here's three questions I want to answer:

1. How do you generate a uniformly random integer $N \in \{0, \dots, 2^N - 1\}?$
2. How do you generate a uniformly random integer $N \in \{0, \dots, M\}$ where $M$ is not necessarily a power of $2$?
3. How do you generate a uniformly random real number in $N \in[0, 1]$?

Question 1

A first instinct answer to this question would be to generate $N$ independent random bits, and concatnate them together to get the base 2 representation of the integer we return. But does this follow uniform distribution? Let $B_1, B_2, \ldots, B_N$ be independent random bits we generated. Define the random integer we return as $$X = \sum_{i=0}^{N-1} B_i \cdot 2^i$$ For any integer $k \in \{0, 1, \ldots, 2^N - 1\}$, there exists a unique binary representation: $$k = \sum_{i=0}^{N-1} b_i \cdot 2^i$$ where each $b_i \in \{0, 1\}$ is the $i$-th bit of $k$.

The probability that $X = k$ is: \begin{align*} \mathbb{P}[X = k] &= \mathbb{P}[B_0 = b_0, B_1 = b_1, \ldots, B_{N-1} = b_{N-1}] \\ &= \mathbb{P}[B_0 = b_0] \cdot \mathbb{P}[B_1 = b_1] \cdots \mathbb{P}[B_{N-1} = b_{N-1}] \quad \text{(by independence)} \\ &= \frac{1}{2} \cdot \frac{1}{2} \cdots \frac{1}{2} \quad \text{($N$ times)} \\ &= \frac{1}{2^N} \end{align*}

which is exactly the uniform distribution. So first instinct ended up being right.

Question 2

Now let's tackle question 2: how do we generate a uniformly random integer in $\{0, 1, \ldots, M\}$ where $M$ is not necessarily a power of 2? Here's where instinct fails. If we simply generate $N$ bits for some fixed $N$, we get $2^N$ possible outcomes. If $M + 1$ is not a power of $2$, then $2^N$ doesn't divide evenly into the $M + 1$ outcomes we want, so some outcomes would be more likely than others.

Here's where rejection sampling comes in to save the day. I claim that the following algorithm gives us what we want:

1. Find the smallest integer $N$ such that $2^N > M$
2. Generate a random integer $X \in \{0, 1, \ldots, 2^N - 1\}$ using $N$ random bits
3. If $X \leq M$, accept and return $X$
4. If $X > M$, reject and go back to step 2

Let's check that this does work. Let $A$ denote the event that we accept (i.e., $X \leq M$). For any $k \in \{0, 1, \ldots, M\}$:

\begin{align*} \mathbb{P}[\text{output} = k] &= \mathbb{P}[X = k \mid A] \\ &= \frac{\mathbb{P}[X = k \text{ and } A]}{\mathbb{P}[A]} \quad \text{(definition of conditional probability)} \\ &= \frac{\mathbb{P}[X = k]}{\mathbb{P}[A]} \quad \text{(since $k \leq M$ implies $A$)} \\ &= \frac{1/2^N}{\mathbb{P}[A]} \quad \text{(from question 1, $X$ is uniform on $\{0, \ldots, 2^N-1\}$)} \end{align*}

Now, the acceptance probability is: \begin{align*} \mathbb{P}[A] &= \mathbb{P}[X \leq M] \\ &= \sum_{i=0}^{M} \mathbb{P}[X = i] \\ &= \sum_{i=0}^{M} \frac{1}{2^N} \\ &= \frac{M + 1}{2^N} \end{align*}

Substituting back: \begin{align*} \mathbb{P}[\text{output} = k] &= \frac{1/2^N}{(M+1)/2^N} \\ &= \frac{1}{M + 1} \end{align*}

Since this holds for all $k \in \{0, 1, \ldots, M\}$, the output is uniformly distributed.

Question 3

Finally, let's address question 3: how do we generate a uniformly random real number in $[0, 1]$? This one is a bit tricky. There are uncountably infinitely many real numbers in $[0,1]$, but we can only generate finitely many bits in practice. So we need to be careful about what we mean by "uniform random real number".

Let's go to Theory Land

We know that every real number $r \in [0, 1]$ can be represented as a binary expansion: $$r = \sum_{i=1}^{\infty} \frac{B_i}{2^i} = 0.B_1B_2B_3\ldots$$

where each $B_i \in \{0, 1\}$. I claim that if $B_1, B_2, B_3, \ldots$ are independent uniform random bits then $$U = \sum_{i=1}^{\infty} \frac{B_i}{2^i}$$ is uniformly distributed on $[0, 1]$.

I will only give a sketch of this proof because it does get quite technical. Feel free to skip this part if you are not familiar with probability distributions over continuous space. But we need to show that for any interval $[a, b] \subseteq [0, 1]$: $$\mathbb{P}[U \in [a, b]] = b - a$$ Let $k \in \mathbb{N}$ be arbitrary. We can partition the interval $[0, 1]$ into $2^k$ intervals: $$I_j = \left[\frac{j}{2^k}, \frac{j+1}{2^k}\right) \quad \text{for } j = 0, 1, \ldots, 2^k - 1$$

The first $k$ bits $(B_1, \ldots, B_k)$ of $U$ determine which $I_j$ $U$ falls into. Specifically: $$U \in I_j = \left[\frac{j}{2^k}, \frac{j+1}{2^k}\right) \iff \sum_{i=1}^{k} B_i \cdot 2^{-i} = \frac{j}{2^k}$$

Since each of the $2^k$ possible bit patterns $(B_1, \ldots, B_k)$ occurs with probability $\frac{1}{2^k}$, the probability $U \in I_j$ has probability $\frac{1}{2^k}$ for all $j$, which also equals the length of $I_j$

For a general interval $[a, b] \subseteq [0, 1]$ and a fixed $k$, we can take the infinite union and approximate $[a, b]$ as $$ [a, b] \approx \bigcup_{j \in \mathbb{N}}^{\infty} I_j $$ As $k \to \infty$, this approximation becomes exact, giving: $$\mathbb{P}[U \in [a, b]] = b - a$$ Note that there is more careful argument to be done here, but I am skipping it because this is a proof sketch. Therefore, $U$ is uniformly distributed on $[0, 1]$.

Back to reality

But in practice, we can't generate infinitely many bits. Instead, we can generate $k$ bits and compute: $$U_k = \sum_{i=1}^{k} \frac{B_i}{2^i}$$ This gives us a random number with $k$ bits of precision, uniformly distributed on the discrete set: $$\left\{0, \frac{1}{2^k}, \frac{2}{2^k}, \ldots, \frac{2^k - 1}{2^k}\right\}$$ But, the error between $U_k$ and the true infinite expansion $U$ is bounded by: $$|U - U_k| = \left|\sum_{i=k+1}^{\infty} \frac{B_i}{2^i}\right| \leq \sum_{i=k+1}^{\infty} \frac{1}{2^i} = \frac{1}{2^k}$$ So with for example $k = 53$ bits (standard double precision), we get an error at most $2^{-53} \approx 1.1 \times 10^{-16}$, which is usually more than enough for practical applications.

Arbitrary probability distribution $\pi$

Great, we can now sample form the uniform distribution. But let's say I have some arbitrary distribution $\pi$ on my finite state space $\cal{X} = {x_1, x_2, \dots, x_N}$. How do I draw a sample $x \in \cal{X}$ such that $$ \mathbb{P}[X = x] = \pi(x) $$

Well, since we can sample from the uniform distribution $[0, 1]$, let's try to use that. We can "partition" the uniform distribution $[0, 1]$ into intervals, where each interval has length equal to the probability we want for each outcome. Then, we sample uniformly from $[0, 1]$ and see which interval we land in.

Imagine a number line from 0 to 1. We divide it into segments:

• Segment 1: $[0, \pi(x_1))$ has length $\pi(x_1)$
• Segment 2: $[\pi(x_1), \pi(x_1) + \pi(x_2))$ has length $\pi(x_2)$
• Segment 3: $[\pi(x_1) + \pi(x_2), \pi(x_1) + \pi(x_2) + \pi(x_3))$ has length $\pi(x_3)$
• And so on...

When we sample uniformly from $[0, 1]$, the probability of landing in segment $i$ is exactly $\pi(x_i)$ (since the segment has length $\pi(x_i)$). So if we return $x_i$ whenever we land in segment $i$, we get the desired distribution. For example, if $\cal{X} = \{x_1, x_2, x_3, x_4\}$ and $\pi = [0.15, 0.25, 0.20, 0.30, 0.10]$ then we can segment the $[0, 1]$ interval as

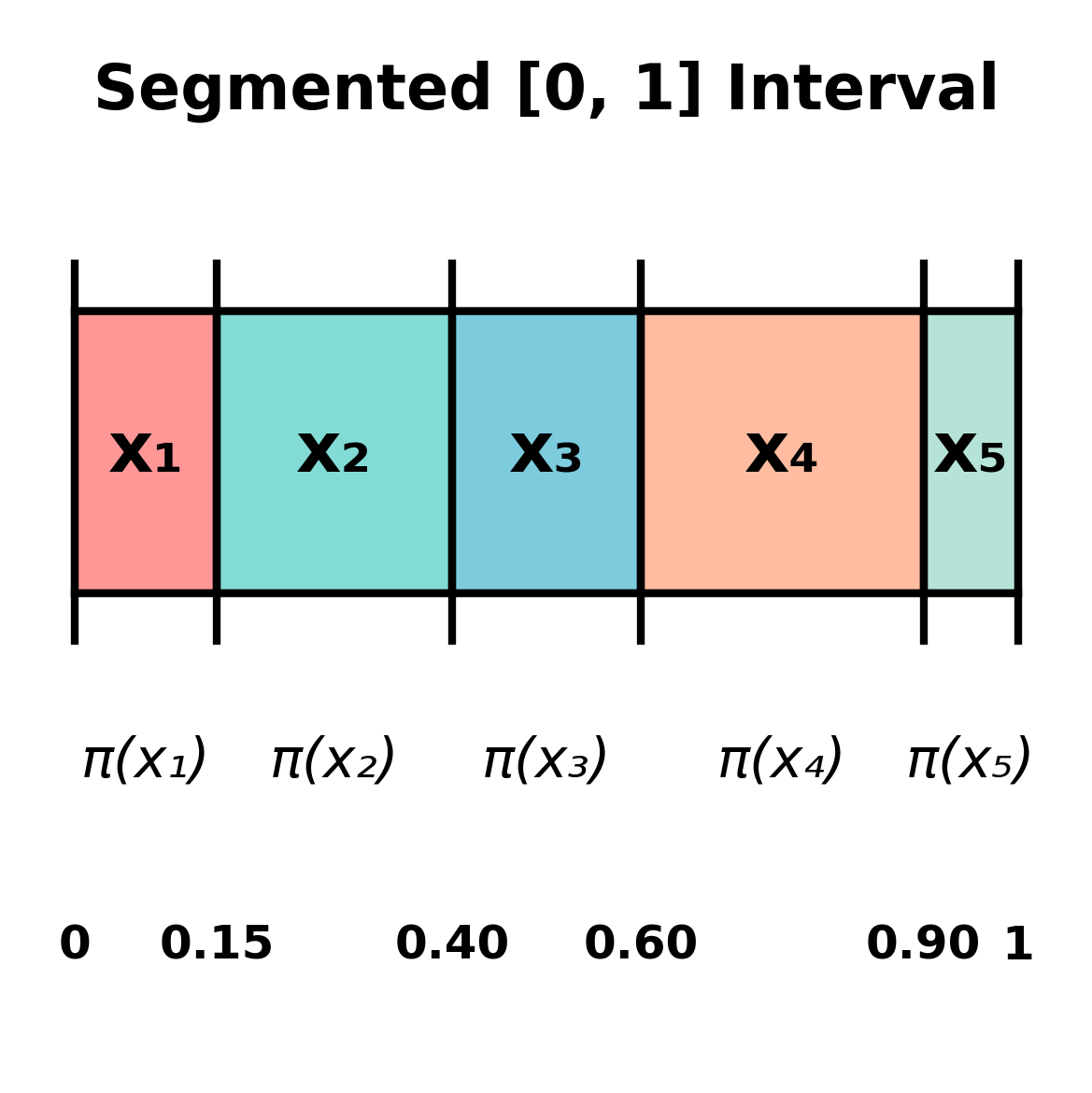
Then we can generate a uniform random number $U \in [0, 1]$, and return value in the segment that $U$ belongs to. By this point, you should first convince yourself that this algorithm works. But if you are curious, Let $U \sim \text{Uniform}[0, 1]$. Define the cumulative probabilities: $$F_i = \sum_{j=1}^{i} \pi(x_j) \quad \text{for } i = 1, 2, \ldots, N$$ with $F_0 = 0$. Our algorithm returns $x_i$ when $U$ falls in the interval $[F_{i-1}, F_i)$. The probability of this event is: $$\mathbb{P}[\text{output} = x_i] = \mathbb{P}[F_{i-1} \leq U < F_i] = F_i - F_{i-1} = \pi(x_i)$$ where the second equality uses the fact that $U$ is uniform on $[0,1]$, so $\mathbb{P}[a \leq U < b] = b - a$. Therefore, our algorithm produces samples distributed according to $\pi$. Great, problem solved!

Application: Language Model Text Generation

One of the most important applications of sampling from discrete distributions is in large language models (LLMs) like GPT, Claude, and others. When a language model generates text, it doesn't just pick the most likely next word. Instead, at each step:

1. The model computes a probability distribution $\pi$ over all possible next tokens (words or subwords) in its vocabulary
2. The model samples a token from this distribution
3. This token is added to the sequence, and the process repeats

For example, suppose we're generating text after the prompt "The weather today is" and the model's vocabulary contains 50,000 tokens. The model might output probabilities like:

Token	Probability
"sunny"	0.35
"rainy"	0.20
"cloudy"	0.15
"beautiful"	0.12
"cold"	0.08
...	...
(other 49,995 tokens)	0.10 (combined)

Using our method, we can sample from this distribution to pick the next token!

import numpy as np

# pi a vector in R^N such that pi_i = PP[X = x_i]
def sample(pi):
    intervals = np.cumsum(pi)
    u = np.random.uniform(0, 1)

    index = np.searchsorted(intervals, u)

    return index

vocab = [
    "the", "a", "and", "is", "with", "to", "for", "of",
    "sunny", "rainy", "cloudy", "stormy", "beautiful", "cold", "warm", "pleasant",
    "weather", "sky", "day", "morning", "afternoon", "evening", "wind", "temperature",
    "outside", "perfect", "great", "bit", "little", "very", "quite", "extremely"
]

# Assign rough frequency weights (higher for common words)
# This is a toy example, so these probabilities will
# be quite bad
weights = np.array([
    # Function words (frequent)
    10, 6, 6, 8, 4, 4, 3, 4,
    # Weather adjectives (moderate)
    5, 4, 4, 3, 5, 3, 3, 4,
    # Nouns / context (moderate)
    4, 3, 4, 3, 3, 2, 2, 2,
    # Activity / modifiers (less frequent)
    2, 2, 2, 1, 1, 2, 1, 1
], dtype=float)

pi = weights / np.sum(weights)

def generate_text(prompt, vocab, pi, num_tokens=10):
    text = prompt
    for _ in range(num_tokens):
        idx = sample(pi)
        next_token = vocab[idx]
        text += " " + next_token

    return text

print(generate_text("The weather this evening is", vocab, pi))

The weather this evening is is beautiful sky cold and for morning beautiful the day