Sending Messages over Noisy Channels

A fundemental problem in computer science and electrical engineering is sending messages over noisy channels. For example, all messages sent over the internet have to eventually be transmitted over physical channels (copper wires or fiber optic cables), and these channels can be damaged.

I recently came across a method to reduce this problem to a purely mathematical one - the sphere packing problem, which aims to find the densest packing of non-overlapping $n$ dimensional spheres in a given space.

An illustration of a dense sphere packing in a cubic space.

Signals and Code

But first, let's define the noisy channel problem more formally. Let $T > 0$ be a fixed length of time corresponding to the length of a signal transmission.

Define a signal to be a continuous function $s: [0, T] \to \mathbb{R}$, where $s(t)$ is the amplitude of the signal at time $t$, and the frequencies do not surpass some fixed limit $W$. Think of $s(t)$ as the voltage of the signal at time $t$ (for copper wires), or the intensity of a light signal at time $t$ (for fiber optic cables).

Define a code to be a finite set of signals $\{s_1, s_2, \ldots, s_n\}$. This can be thought of as a symbolic alphabet for the two computers to communicate with via the channel. A simple example of a code is the set of signals $\{s_1(t) = 1, s_2(t) = -1\}$, which can be used to send binary messages over a channel.

The Shannon-Nyquist Sampling Theorem states that any signal $s(t)$ with frequencies less than $W$ can be uniquely represented by a finite set of samples $\{s(0), s(\frac{1}{W}), s(\frac{1}{2W}), \ldots, s(\frac{n-1}{2W})\}$, where $n = 2WT$. This means that we can represent any signal $s(t)$ as a vector $\vec{s} \in \mathbb{R}^n$, and any code as a finite subset $C \subseteq \mathbb{R}^n$, where each element of $C$ is a vector representing a signal in the code.

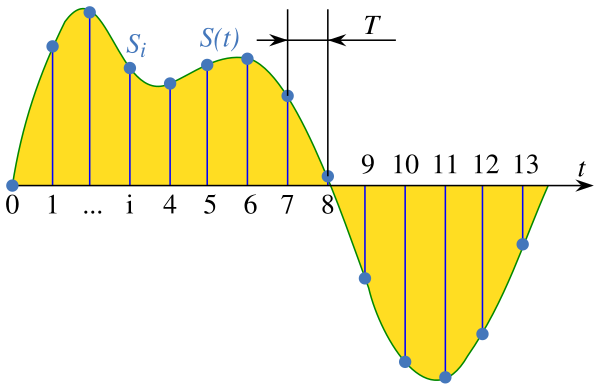
The continuous signal $s(t)$ is represented by the discrete samples.

The Noisy Channel

However, in the real world, the sent signal $\vec{s}$ is almost never the same as the received signal $\vec{r}$. This is because the channel introduces noise, which we can think of as a random perturbation to the signal. So, we will assume that the received signal $\vec{r}$ is the sent signal $\vec{s}$ plus some noise $\vec{z}$, where $\vec{z}$ is a random vector with Gaussian entries (i.e., each $z_i$ is drawn from a normal distribution with mean 0 and variance $\sigma^2$).

Suppose the sender wants to send a signal $\vec{s}$ over the channel, and the receiver receives a signal $\vec{r} = \vec{s} + \vec{z}$. The receiver wants to determine which signal was sent, but the noise makes this difficult. One way to do this is to choose the signal in the code that is closest to the received signal $\vec{r}$ i.e., pick an $\vec{s}$ such that $||\vec{r} - \vec{s}||_2$ is minimized. However, consider the case when two signals in the code overlap like below. The noise could cause the received signal to be equidistant from both signals, making it impossible for the receiver to determine which signal was sent.

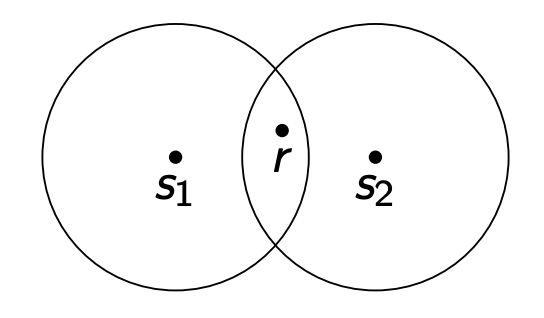
Which signal does r correspond to?

But, recall that each component $z_i$ of $z$ is Gaussian, so $\mathbb{P}[-2\sigma \leq z_i \leq 2\sigma] \approx 95\%$. Now, this means $\mathbb{P}[\|\vec{z}\|_2 \leq 2\sigma\sqrt{n}] \approx 95\%$. So, the distance $$|| \vec{r} - \vec{s}||_2 = ||(\vec{s} + \vec{z}) - \vec{s}||_2 = ||\vec{z}||_2 \leq 2\sigma\sqrt{n}$$ with high probability. This means that if we choose the code such that the minimum distance between any two signals in the code is at least $4\sigma\sqrt{n}$, then the receiver can correctly decode the signal with high probability. Suddenly, this problem is now reduced to finding a packing of spheres in $\mathbb{R}^n$ such that the minimum distance between any two spheres is at least $4\sigma\sqrt{n}$, which of course is the sphere packing problem!

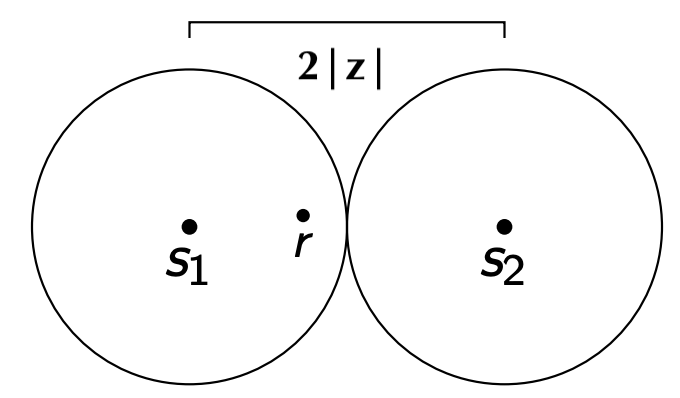
These signals are sufficiently far apart.

Epilogue

The attentive reader might have noticed that a naive solution to the Noisy Channel problem is to choose a code such that minimum distance between any two signals is as far as possible. However, this is not feasible in practice. Recall the average power) exerted by a discrete signal $\vec{s}$ is given by: $$ P = \frac{1}{T} \sum_{i=1}^n |s_i|^2 = \frac{1}{T} ||\vec{s}||_2^2 $$

Therefore, the power required to transmit a signal $\vec{s}$ is proportional to the L2 norm of the signal squared. So, if we choose a code such that the minimum distance between any two signals is very large, then the power required to transmit the signal will also be very large, which is not desirable. However, if we choose a code whose associated spheres are packed as densely as possible, then we can minimize the power required to transmit the signal, while still ensuring that the receiver can correctly decode the signal with high probability.